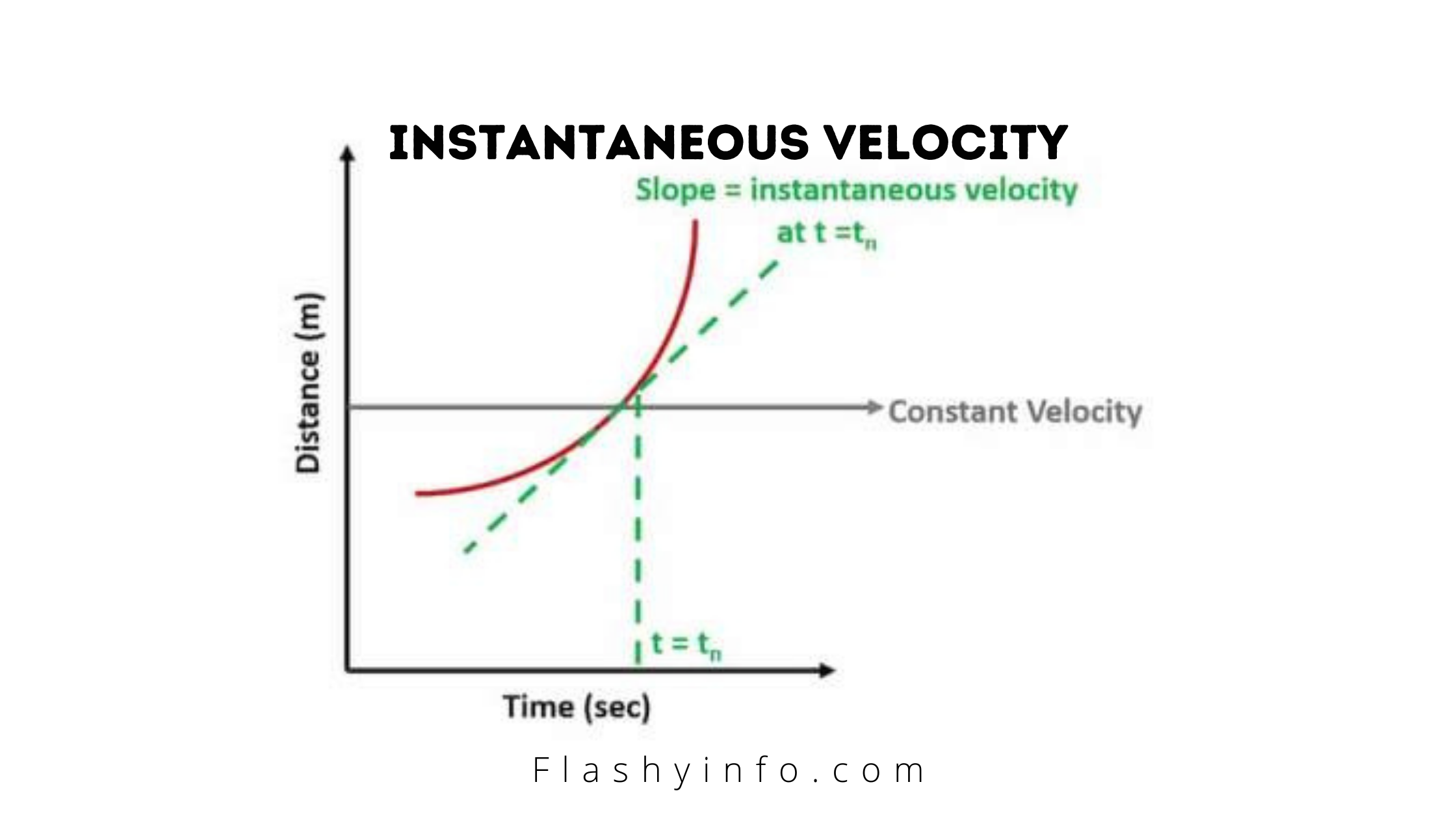
A Discussion About Instantaneous Velocity
The velocity of an object at a certain time in history is called its instantaneous velocity. The instantaneous velocity is the velocity in a given direction at a given time. We can calculate it by finding the force on an object in its location, which changes with time. The results can be in the form of graphs or mathematical expressions. This is often used in engineering applications, especially mechanics, in the application of fluids to reduce friction and improve performance.
Definition of Instantaneous Velocity in Physics

In physics, the instantaneous velocity of an object is the average energy required to move it from point A to point B. Thus, we can say that the magnitude of the velocity is proportional to the energy change. With the time approaching zero. In cases where the magnitude of the velocity does not change with time. This is the static magnitude. Thus, if a mass at rest has no change in velocity with time. Then we call it zero time, or stationary.
Related: THE ROLE OF KINETIC ENERGY IN AERODYNAMICS
The components of the instantaneous velocity are the change in velocity with time. The time-averaged velocity, and the components of the change in momentum with time. Collectively termed the time-averaged mean velocity. In some cases, we write these components as t 1/t 2 | velocity | time | component | time average. We can neglect The first component. This means that the only thing left to be accounted for is the second component of the acceleration. This is usually done by dividing the change in velocity with time by the time average, thus: t 1/t 2.
When Instantaneous Velocity is Zero

In the case of a system of constant mass. The instantaneous velocity at any time will be the same as the average velocity over the system. This is true for fluids in which the density is the same, whether the system is static or moving. Thus, for instance, in a free-falling equilibrium, the instantaneous velocity will be zero over the course of 50 kilometers. In systems of constant mass, such as in a rocket. The value of the instantaneous velocity is zero over the entire flight.
The Formula for Finding the Instantaneous velocity
The instantaneous velocity will be a function of the magnitude of the launch angle and the altitude above the earth’s atmosphere. For higher launch angles and higher altitudes, this function will be greater than unity. Thus, for a launch at an altitude of say ten meters, where the impulse produced is tens of meters/second, the instantaneous velocity will be approximately half a meter per second. And if the angle of launch is thirty degrees, then the impulse will be about one.5 seconds/second. The formula for finding the instantaneous velocity is:

Thus, for any set of coordinates on the x-axis, the instantaneous velocity is a function of the x-intercept and the time it takes for the average velocity to approach zero. The formula to find the instantaneous velocity from these x-intercepts is: Where T is the time and Tb is the constant air temperature. If the slope of the tangent line to the normal curve on the earth’s surface is non-zero, then the instantaneous velocity will also be non-zero. For any set of coordinates on the x-axis, the instantaneous velocity will be equal to the impulse generated when the average velocity approaches zero at that location.
Also Read: FORMS OF SHEAR STRESS IN SURFACES
How to Find Immediate VS Continuous Function Relationships in Physics
Instantaneous velocity is a constant function of time. It is determined by a particular time-dependent function f(z), which defines the tangential velocity of a particle s at any time during its motion. By taking the derivative of this position function, which gives the orthogonal function of instantaneous velocity v, a system may calculate it at some specific time T. Thus we get the integral formula for finding velocity. The integral formula is used to solve the system of simultaneous variables. This involves first finding the system of linear equations. Such as Eq. which determines the characteristic function and then solves for x, the stationary term.
The First Step to Calculate Instantaneous Velocity
The first step is to fit a data set. For example, the set of real x-ray results obtained after taking a snapshot of an object at a certain time T. The second step is to set up a function. That models the variable v such that the function can be integrated over time using a uniform velocity model. The third step is the integration of the function through the uniform velocity model. Thus by fitting the function to the data we get a set of x-ray results at time T. The last step is then to plot the function on a graph of a time-dependent function.
How to Find Velocity
To find velocity on a straight line, there are two methods, both of them are quite successful and accurate.

Using Identity Function
One of them is by using the identity function. This function is very much like the identity function. When we use it on a horizontal x-axis, it gives us the value of the horizontal position of zero on the x-axis. Then by plotting it against the point where the horizontal derivative of the acceleration gets to be zero. We get a plot of constant velocity. This looks similar to what we see on the time-axis as the uniform velocity.
Plot Against the Time Axis
Another method is to plot it against the time axis. We now have a vector quantity whose direction and fixed magnitude. In general terms, we call the magnitude of the vector its angular velocity. We plot it against the normal to the x-axis and then we get a plot of instantaneous speed. It looks like a curved line that represents the change in momentum of an object over a period of time.

Lagrange Equation
One can also calculate the instantaneous velocity and other such quantities by means of a Lagrange Equation. James Clerk Maxwell discovered The Lagrange Equation. He had studied electrostatic repulsion and found a relationship between the initial displacement and the resultant velocity after some time t squared. The equation then says that for a particle P at initial displacement, t equals L/S. Let us now calculate the Lagrange Equation for the same case: P=qy, where y is the initial displacement. Therefore we can conclude that the particles have momentum. But it does not give any time taken for them to change their momentum.
For More Articles Visit: Flashy Info